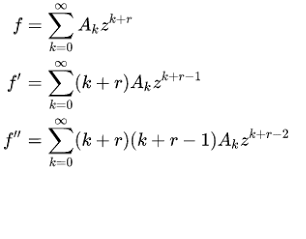The notes above is Fall 2020 version. Here is the spring 2019 version.

Both set of notes are mostly following the textbook/coursenote. Below is a proof of a result.

Some good properties that prof assumed we know (maybe we don’t) from previous courses:

$$ \mathcal L[tf(t)] = -{d\over ds}\mathcal L[f] $$

Proof:

$$ \begin{aligned} {d\over ds} F(s) &= {d\over ds} \int _ 0^\infty e^{-st} f(t)dt \\ &= \int _ 0^\infty {d\over ds}e^{-st}f(t)dt \\ &= \int _ 0^\infty -t e^{-st}f(t)dt \\ &= -\int _0 ^\infty e^{-st}(tf(t))dt \\ &= -\mathcal L [tf(t)] \end{aligned} $$